Shor’s Error Correction Algorithm

Quantum computing is still very much in its infancy. Algorithms run on real hardware may produce wildly inaccurate outputs. Besides the measurements themselves being imprecise, errors arise due to environmental factors such as vibration, temperature fluctuation, and electromagnetism. Therefore, in addition to improving the physical systems over time, there currently exist error correction algorithms designed to increase accuracy.

Because error correction requires additional quantum bits (qubits), and because the largest quantum computer available to me has only 14 qubits, I had to experiment with an algorithm that requires few qubits. Basic Quantum Teleportation only requires 3 qubits, so I decided to test error correction on this algorithm first.

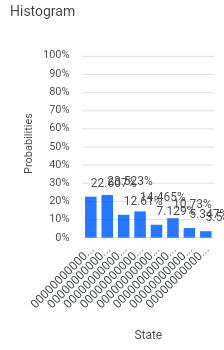
This was the result of my Quantum Teleportation experiment on real hardware. Please read the original blog article for details, but the executive summary is that the left half of the histogram indicates successful teleportation and the right half indicates failure. Of note, the bars (representing probabilities) are higher on the left side and lower on the right side. Keep that in mind as you read on.

This is my Quantum Teleportation experiment with Shor’s Error Correction Algorithm mixed into it. I selected Shor’s algorithm because it was the first quantum error correction algorithm and it seems to be the most documented. There are other quantum error correction algorithms that I also intend to experiment with in the near future.

The basic premise of quantum error correction is that you can improve accuracy by encoding one quantum state on multiple qubits. Shor’s algorithm uses 9 qubits to protect agains bit flips (0 to 1, 1 to 0) and sign flips (+ to -, – to +), but this should be possible with as few as 5 qubits. It is important to note that this pertains specifically to single-qubit error correction. This statement also does not pertain to codes, which look like they might require fewer qubits, but I have not yet found a full implementation of one.

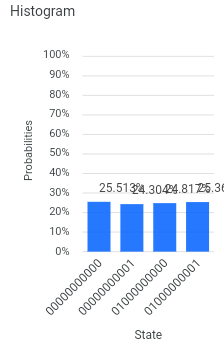
The result, even on a simulator, was clearly wrong. Every possible outcome, including failures, had just about equal probability.

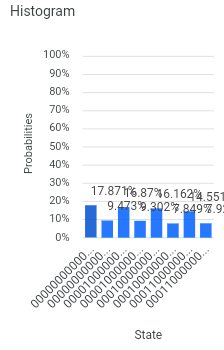
On real hardware, it didn’t look much better. This histogram has hints of the left-to-right decline that we are looking for, but success and failure still have relatively equal probabilities.

I suspected that the problem was the Z gate. The quantum state being teleported had a Z gate then an H gate applied to it. But, the CX and CCX gates of Shor’s algorithm don’t address the Z gate.

Therefore, I modified Shor’s algorithm. Everywhere I saw an H gate I added a Z gate. And everywhere I saw CX or CCX gates I added CZ or CCZ gates, respectively.

OPENQASM 2.0;
include "qelib1.inc";
qreg q[11];
creg c[11];

z q[0];
h q[0]; // secret unitary: hz

barrier q; // Shor's error correction algorithm
cx q[0], q[3];
cx q[0], q[6];
cz q[0], q[3];
cz q[0], q[6];
h q[0];
h q[3];
h q[6];
z q[0];
z q[3];
z q[6];
cx q[0], q[1];
cx q[0], q[2];
cx q[3], q[4];
cx q[3], q[5];
cx q[6], q[7];
cx q[6], q[8];
cz q[0], q[1];
cz q[0], q[2];
cz q[3], q[4];
cz q[3], q[5];
cz q[6], q[7];
cz q[6], q[8];

// Alice starts with qubit 9.
// Bob starts with qubit 10.
// Alice is given qubit 0.
// Bob is given error-correcting qubits 1-8.
// Alice and Bob do not know what has been done to qubit 0.

barrier q; // Alice and Bob entangle their starting qubits.
h q[9];
cx q[9], q[10];

// Alice keeps qubits 0 and 9.
// Bob leaves with qubits 1-8 and 10.

barrier q; // Alice teleports the quantum state of qubit 0 to Bob's qubit.
cx q[0], q[9];
measure q[9] -> c[9];
h q[0];
cx q[9], q[10];
measure q[0] -> c[0];
cz q[0], q[10];

barrier q; // Bob corrects for bit flips and sign flips
cx q[10], q[1];
cx q[10], q[2];
cx q[3], q[4];
cx q[3], q[5];
cx q[6], q[7];
cx q[6], q[8];
cz q[10], q[1];
cz q[10], q[2];
cz q[3], q[4];
cz q[3], q[5];
cz q[6], q[7];
cz q[6], q[8];
ccx q[1], q[2], q[10];
ccx q[5], q[4], q[3];
ccx q[8], q[7], q[6];
barrier q; // start CCZ gates
h q[10];
ccx q[1], q[2], q[10];
h q[10];
h q[3];
ccx q[5], q[4], q[3];
h q[3];
h q[6];
ccx q[8], q[7], q[6];
h q[6];
barrier q; // end CCZ gates
h q[10];
h q[3];
h q[6];
z q[10];
z q[3];
z q[6];
cx q[10], q[3];
cx q[10], q[6];
cz q[10], q[3];
cz q[10], q[6];
ccx q[3], q[6], q[10];
h q[10];
ccx q[3], q[6], q[10];
h q[10];

barrier q; // Based on Alice's measurements, Bob reverses the secret unitary.
// 00 do nothing
// 01 apply X
// 10 apply Z
// 11 apply ZX
h q[10];
z q[10];
measure q[10] -> c[10]; // A 0 i

My modified code is about twice as long as Shor’s algorithm will typically be if you find it elsewhere.

For those looking for CCZ gates and not finding them, they don’t exist on IBM Q. Therefore, they have to be created out of other gates. For this experiment, CCZ gates consist of 3 other gates: H, then CCX, and then another H.

From left to right, by block:

1. Apply the secret unitary
2. Add protection against single-qubit errors
3. Entangle Alice’s and Bob’s qubits
4. Teleport the secret unitary
5. Apply error correction
6. CCZ gates
7. Apply more error correction
8. Reverse the secret unitary on Bob’s qubit, confirming successful teleportation

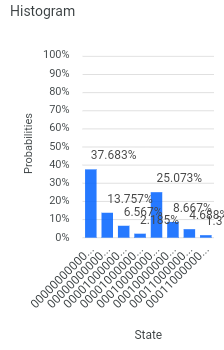
Error correction isn’t perfect either, but this result is interesting. There are 2 sets of left-to-right declination, with successful teleportation on the left and failure on the right. The total probability of success has actually decreased slightly, but the probability of Bob’s qubit having the same measurement as qubit 0 has more than doubled.

Because of the obvious importance of accuracy, quantum error correction is a topic that I will continue to work on. I will still be limited by available hardware, but I can continue to strive to make my results as accurate as possible within that limitation.